

recommends the Wilson or Jeffreys methods for small n and Agresti-Coull, Wilson, or Jeffreys, for larger n as providing more reliable coverage than the alternatives. Conversely, the Clopper-Pearson Exact method is very conservative and tends to produce wider intervals than necessary. Hence, the larger the Z-score, the larger your confidence interval will be. Similarly, for a 99 confidence level, the Z-score is approximately 2.576. the Mean Calculator - Calculates a (90 - 99) estimation of confidence interval for the. This means that if your data is normally distributed, about 95 of values are within 1.96 standard deviations of the mean. X sample mean, s sample standard deviation, zscore Normal. The Wald interval often has inadequate coverage, particularly for small n and values of p close to 0 or 1. For a 95 confidence level, the Z-score is approximately 1.96. "Agresti-Coull" (adjusted Wald) interval and.Binomial (Clopper-Pearson) "exact" method based on the beta distribution.Asymptotic (Wald) method based on a normal approximation.
#90 CONFIDENCE INTERVAL Z SCORE CALCULATOR PLUS#
The program outputs the estimated proportion plus upper and lower limits of the specified confidence interval, using 5 alternative calculation methods decribed and discussed in Brown, LD, Cat, TT and DasGupta, A (2001). Calculating the Z score for a 90 confidence interval, we have We check the value of probability 0. A z-score for a 95 confidence interval for a large enough sample size (30 or more) is 1.96. Inputs are the sample size and number of positive results, the desired level of confidence in the estimate and the number of decimal places required in the answer.
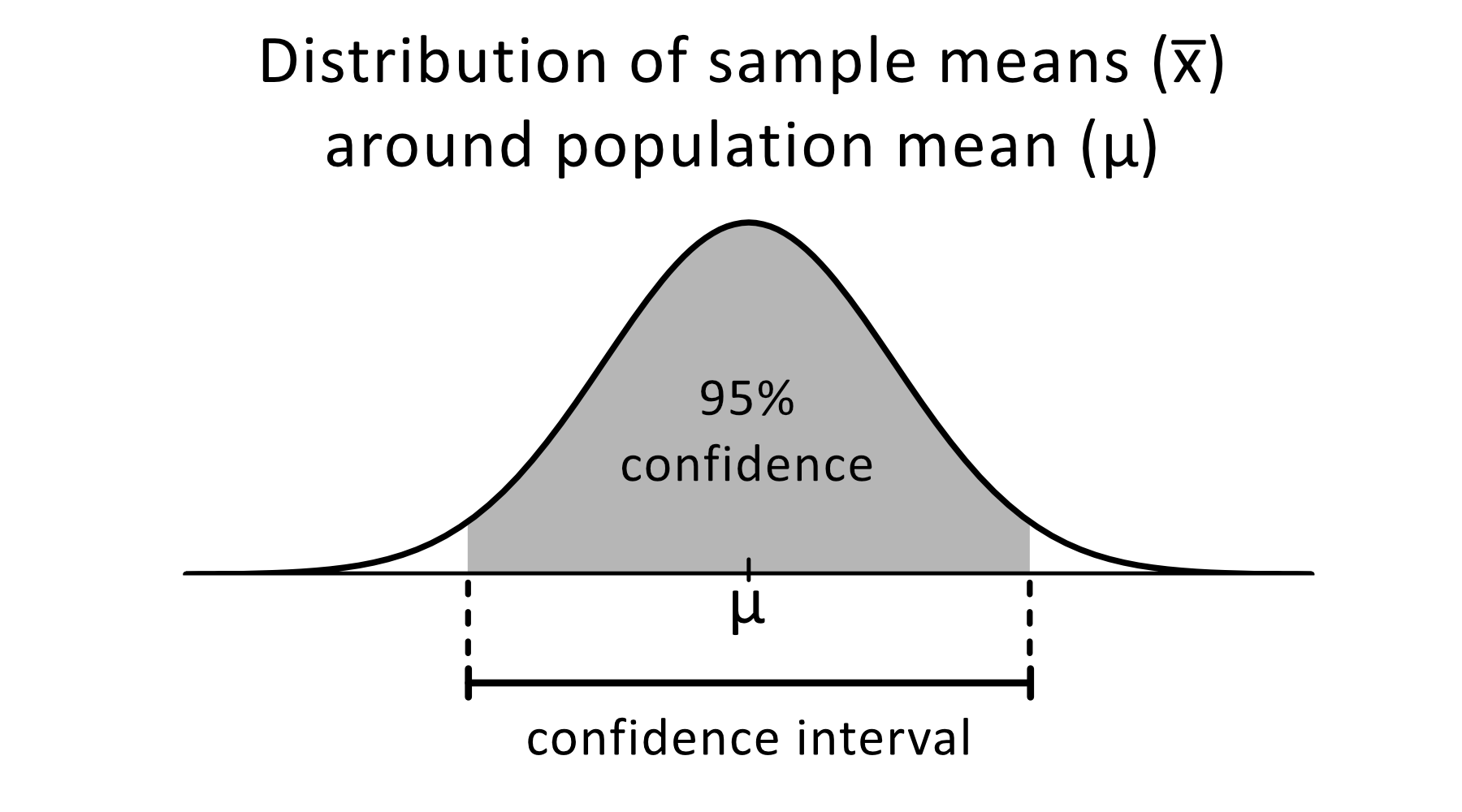
This utility calculates confidence limits for a population proportion for a specified level of confidence.


 0 kommentar(er)
0 kommentar(er)
